2110. 供水设施
X星球的居民点很多。Pear决定修建一个浩大的水利工程,以解决他管辖的N个居民点的供水问题。现在一共有N个水塔,同时也有N个居民点,居民点在北侧从1号到N号自西向东排成一排;水塔在南侧也从1号到N号自西向东排成一排。
N条单向输水线(有水泵动力),将水从南侧的水塔引到北侧对应的居民点。
我们不妨将居民点和水塔都看做平面上的点,居民点坐标为(1,K)~(N,K),水塔为(1,0)~(N,0)。
除了N条纵向输水线以外,还有M条单向的横向输水线,连接(Xi,Yi)和((Xi)+1,Yi)或者(Xi,Yi)和((Xi)-1,Yi)。前者被称为向右的水路,而后者是向左的。不会有两条水路重叠,即便它们方向不同。
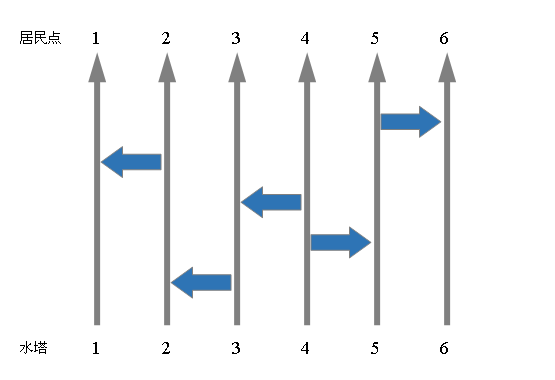
布局的示意图如:【p1.png】所示。
显然,每个水塔的水都可以到达若干个居民点(而不仅仅是对应的那个)。例如上图中,4号水塔可以到达3、4、5、6四个居民点。
现在Pear决定在此基础上,再修建一条横向单向输水线。为了方便考虑,Pear认为这条水路应当是自左向右的,也就是连接了一个点和它右侧的点(例如上图中连接5和6两个纵线的横向水路)。
Pear的目标是,修建了这条水路之后,能有尽可能多对水塔和居民点之间能到达。换句话说,设修建之后第i个水塔能到达Ai个点,你要最大化A1+A2+...+An。
根据定义,这条路必须和X轴平行,但Y坐标不一定要是整数。注意:虽然输入中没有重叠的水路,但是你的方案可以将新修的输水线路与已有的水路重叠。
输入
输入第一行包含三个正整数N,M,K,含义如题面所述:N是纵向线数,M横向线数,K是居民点纵坐标。
接下来M行,每行三个整数。前两个正整数Xi Yi表示水路的起点坐标;
1<=Xi<=N,0<Yi<K。
接下来一个数0或者1,如果是0表示这条水路向左,否则向右。
保证水路都是合法的,也就是不会流向没有定义的地方。
输出
输出一行。是一个正整数,即:题目中要求的最大化的A1+A2+...+An。
样例
| 标准输入 复制文本 |
4 3 2 1 1 1 3 1 0 3 1 1 |
| 标准输出 复制文本 |
11 |
| 标准输入 复制文本 |
7 9 4 2 3 0 7 2 0 6 3 1 6 1 0 2 1 1 3 3 1 5 2 0 2 2 1 7 1 0 |
| 标准输出 复制文本 |
21 |
提示
蓝桥杯-考题-供水设施